맞붙인 오각둥근지붕
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
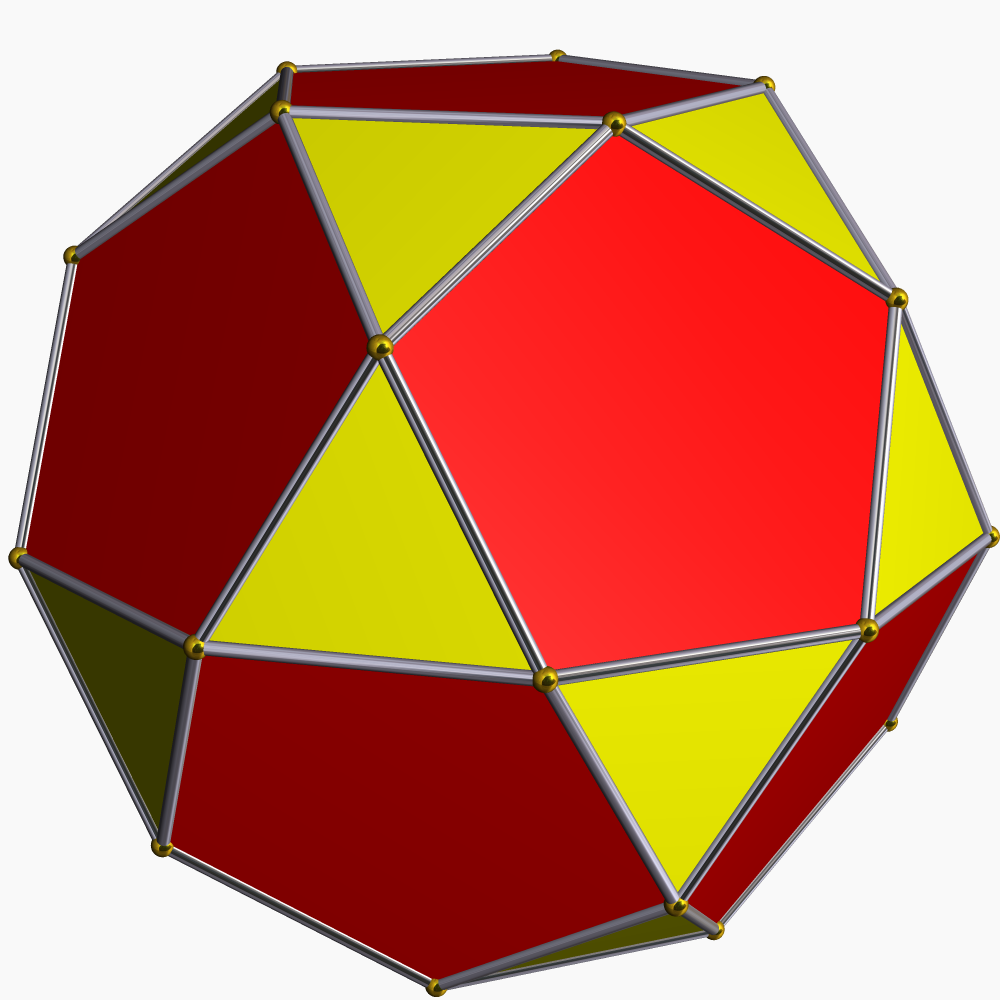
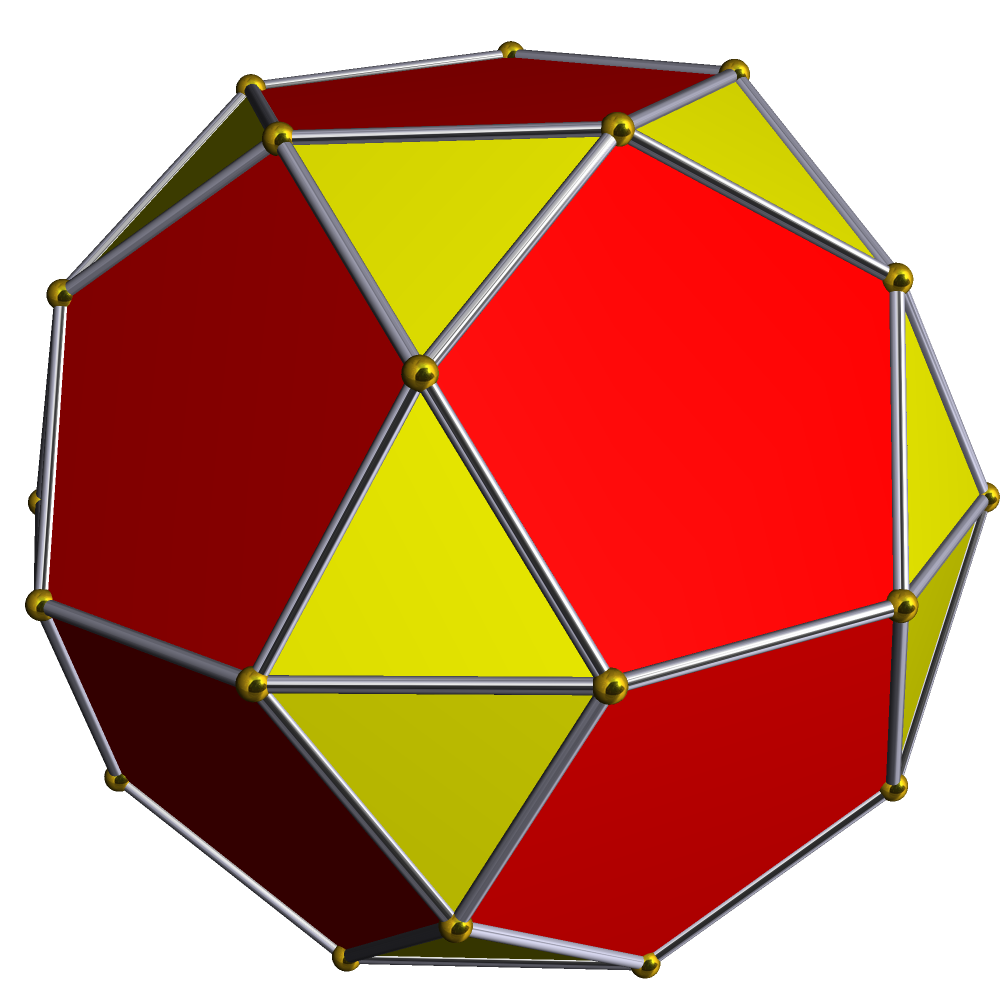
맞붙인 오각둥근지붕은 두 개의 오각둥근지붕을 십각형 면이 서로 겹치도록 연결하여 구성된 다면체이다. 32개의 면, 30개의 꼭짓점, 60개의 모서리를 가지며, 존슨의 다면체 중 34번째에 해당한다. 이십이십면체와 유사하며, 오각둥근지붕을 36° 회전시켜 붙인 십이이십면체와 관련이 있다.
더 읽어볼만한 페이지
2. 구성
맞붙인 오각둥근지붕은 두 개의 오각둥근지붕을 십각형 밑면끼리 서로 붙여서 만든다. 이 다면체는 32개의 면, 30개의 꼭짓점, 60개의 모서리를 갖는다.
맞붙인 오각둥근지붕은 십이이십면체와 관련이 있다. 십이이십면체는 '비틀어 붙인 오각둥근지붕'이라고도 불리며, 오각둥근지붕 두 개를 서로 36도 회전시켜 붙여 만든 아르키메데스의 다면체이다. 맞붙인 오각둥근지붕과의 차이점은, 십이이십면체는 두 오각둥근지붕 중 하나를 36도 회전시켜 오각형 면이 삼각형 면과 마주보게 붙이지만, 맞붙인 오각둥근지붕은 회전 없이 같은 종류의 면(오각형-오각형, 삼각형-삼각형)끼리 마주보게 붙인다는 점이다.
{| class="wikitable"
|align=center|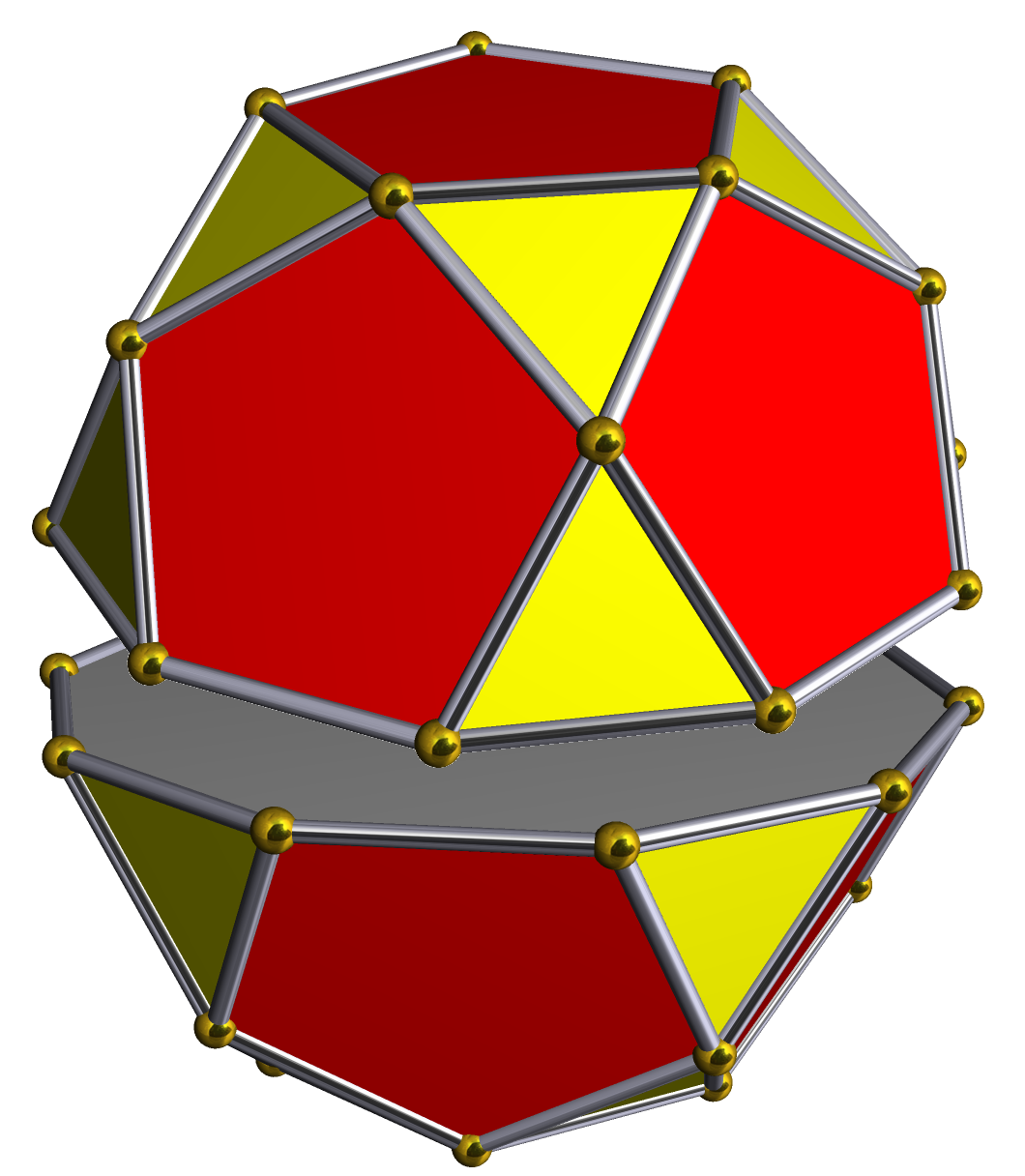
(해체)
|
맞붙인 오각둥근지붕은 모든 면이 정다각형인 볼록 다면체 중 하나인 존슨의 다면체이며, 34번째 존슨의 다면체(J34)이다.
맞붙인 오각둥근지붕(정오각쌍둥근지붕)은 오각둥근지붕 두 개를 밑면끼리 붙여서 만든 존슨의 다면체 (J34)이다. 이 다면체는 32개의 면, 30개의 꼭짓점, 60개의 모서리를 가진다.
|}
맞붙인 오각둥근지붕은 모든 면이 정다각형으로 이루어진 볼록 다면체이므로 존슨의 다면체에 속하며, 34번째 존슨 다면체로 J34로 표기한다.
3. 성질
한 변의 길이를 라고 할 때, 맞붙인 오각둥근지붕의 주요 성질은 아래 표와 같다.
4. 관련 다면체
맞붙인 오각둥근지붕은 오각둥근지붕 두 개를 붙여 만들지만, 한쪽 둥근지붕을 36도 회전시켜 붙인 십이이십면체와 밀접한 관련이 있다. 십이이십면체는 아르키메데스의 다면체이며 '비틀어 붙인 오각둥근지붕'이라고도 불린다. 즉, 맞붙인 오각둥근지붕과 십이이십면체는 동일한 오각둥근지붕 두 개로 구성되지만, 결합 시 회전 여부에서 차이가 있다.
4. 1. 관련 다면체의 예시
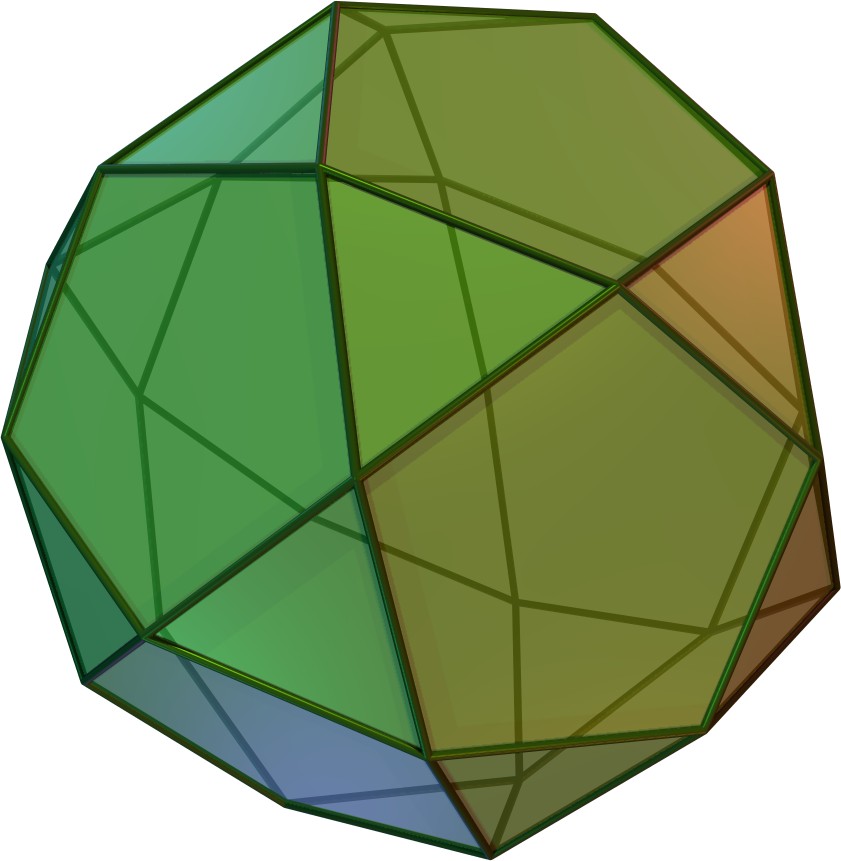
참조
[1]
논문
Regular-faced convex polyhedra
[2]
논문
Johnson solids & their acronyms
https://go.gale.com/[...]
[3]
서적
Integrability, Quantization, and Geometry: II. Quantum Theories and Algebraic Geometry
https://books.google[...]
American Mathematical Society
[4]
간행물
Convex polyhedra with regular faces
본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.
문의하기 : help@durumis.com